The response spectrum method is used to compute inertial response, estimates of response quantities developed for each mode, each direction of excitation and each input, if multiple inputs are considered. The total response is then formed by summing over all modal component, spatial component and excitation component responses. It estimate the structural response to short, nondeterministic, transient dynamic events. Examples of such events are earthquakes and shocks. Since the exact time history of the load is not known, it is difficult to perform a time-dependent analysis.
It is a widely used procedure for performing elastic dynamic seismic analysis, represents the set of the maximum acceleration, velocity or displacement responses of a family of single-degree-of-freedom (SDOF) damped oscillators.
Fig: 1
For a given time period of system, maximum response is picked. This process is continued for all range of possible time periods of SDOF system. Final plot with system time period on x-axis and response quantity on y-axis is the required response spectra pertaining to specified damping ratio and input ground motion as acceleration, velocity or displacement response.
Factor Influencing Response Spectra:
- Damping in the system
- Time period of the system
- Energy release mechanism
Errors in Evaluation of Response Spectrum:
Truncation Error: – In general, a truncation error exists in numerical methods for
integrating differential equations.
Rounding the Time Record: – For earthquake records digitized at irregular time intervals, the integration technique proposed in this report requires rounding of the time record and the attendant error depends on the way the rounding is done. For round-off to 0.005 sec, the average error in spectrum values is expected.
Error Due to Discretization: – In any numerical method of computing the spectra, the response is obtained at a set of discrete points. Since spectral values represent maximum values of response parameters which may not occur at these discrete points, discretization introduces an error which gives spectrum values lower than the true values. Multi degree of freedom (MDOF) systems are usually analyzed using Modal Analysis. A typical MDOF system with ‘n’ degree of freedom. The system when subjected to ground motion undergoes deformations in number of possible ways. These deformed shapes are known as modes of vibration or mode shapes.
In SolidWorks Simulation, we can predict the Displacement, Maximum Stress Induced and frequency with respective mode shapes of the system. with response as acceleration, velocity or displacement input to the system, with irrespective of the system type, the system can be

Regular or Irregular as shown in Fig:2 & Fig:3.
Fig:2(irregular Structure)
Fig:3(Regular)
Regular Structure:
The design shall be approximately symmetrical in plan with respect to two orthogonal axis with flowing assumptions:
- Location of joints with equal spacing in the design.
- No horizontal or vertical irregularity of the structure
- No change in material or shape of the structure cross section.
Irregular Structure:
If the design does not follow any assumptions of the regular system, becomes irregular structure. Most of the mechanical designs are Irregular in nature, as there may be material changes to the main members to improve the strength of the design.
There are different methods that are used for combining the response of each direction of system the methods for MDOF system are as follows:
- Square root of sum of squares (SRSS) Method
- Absolute Sum (ABSSUM) Method
- Complete quadratic combination (CQC) Method
- Naval Research Laboratory (NRL)
Square root of sum of squares (SRSS) Method:
The maximum response is obtained by square root of sum of square of response in each mode of vibration, the effect is calculated for each individual Frequency of the system with the defined response at different directions, these responses are summed up and an averaged.
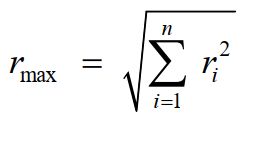
Limitation of SRSS:
- There is a poor estimator of peak responses when applied to systems with closely spaced natural periods.
- Significant errors are caused when working with Irregular system.
Absolute Sum Method:
The peak responses of all the modes are added algebraically, assuming that all modal peaks occur at same time. The maximum response is given by:
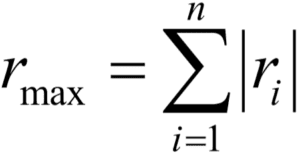
Complete quadratic combination (CQC) Method:
The previously illustrated errors which are inherent in absolute sum or the SRSS method are rectified with CQC, The maximum response from all the modes is calculated as:

![]()
rmax is the maximum response
ri, rj are maximum responses in the ith and jth modes
αij is Cross Modal Coefficient
ξ is Modal Damping Ratio, β is Frequency Ratio [ ]
Naval Research Laboratory (NRL) Method:
The Naval Research Laboratory (NRL) method to combine the peak responses from all mode shapes into overall displacements and stresses. It is modification of the SRSS Method, takes the absolute value of the response for the mode that exhibits the largest response and adds it to the SRSS response of the remaining modes the maximum response from all the modes is calculated as:

Where {uj}max represents the mode with the largest response among all modal responses.
All the above methods discussed are available in SolidWorks Simulation, according to the structure type and the user requirement, we can define the mode combination method as shown in the Fig: 4.
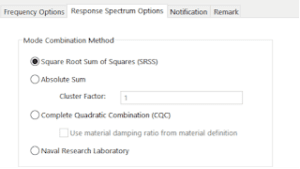
Fig: 4
We had discussed the different mode combination techniques in Response Spectrum, and the purpose of the different techniques and also the model equations of the techniques with their limitations.
THANK YOU FOR READING!